spark机器学习基础统计学知识

服务近2000家企业，依托一系列实践中打磨过的技术和产品，根据企业的具体业务问题和需求，针对性的提供各行业大数据解决方案。

一、矩阵与向量

1.矩阵：按长方阵列排列的实数或复数的集合，在程序中以二位数组存储，矩阵的运算包括（加，减，乘（数乘，叉乘），转置，共轭）

scala中创建矩阵(使用breeze包，mllib中的包创建的矩阵无法做计算)

val jz1 = breeze.linalg.DenseMatrix(Array(1,2,3),Array(4,5,6))

2.向量：既有大小又有方向的量称为向量，矩阵中每一个列可以看做是一个列向量，每一行可以看做是一个行向量，向量的模长看做是向量的大小

向量的N范数为向量内每个元素的N次方和开N次方，P等于2时范数为向量的摸长

scala中创建向量(使用breeze包，mllib中的包创建的向量无法做计算)

var xl1 = breeze.linalg.DenseVector(1,2,3,4) 加法xl1+xl1

二、统计学基础

1.平均数(数学期望是抽样的平均数)

2.方差衡量一组数据的离散率

3.众数：是一组数据中出现次数最多的数数值，可以是0个或多个

1，2，3，4无众数

2, 2, 3,4, 5,众数为2

3，4，5，3，5众数为3和5

4.中位数：为一组数据按大小排序后最中间的那个数（这组数据为偶数时取中间两个值得平均值）

5.scala中使用stat.Statistics.colStats()

6.皮尔逊相关系数：体现两个变量X,Y线性相关性的系数,

stat.Statistics.corr(x,y) //x,y为集合或行向量

7.假设检验(皮尔森卡方检验),先提出假设，然后统计验证这种假设是否能被拒绝

stat.Statistics.chiSqTest(matrix) //参数为矩阵数据

eg ：

男 女

右撇子 127 147

左撇子 19 10

假设性别与左右撇子两个事件相互独立，matrix = |127 147 |

|19 10 |

三、基础算法

回归算法与分类算法类似，区别是回归是线性的分类是离散的

将所有输入分布出来，拟合一条个函数表示这种分布（拟合的过程较训练），根据这个函数的输入求得输出就是回归

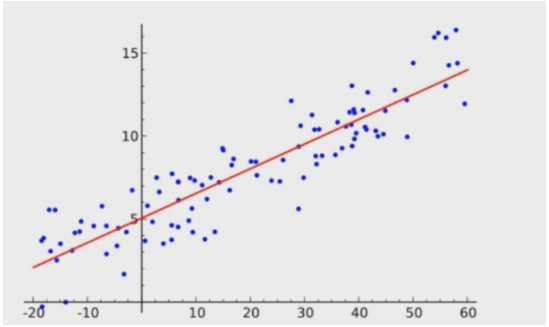
1.线性回归：在回归分析中，自变量与应变量基本满足线性关系就可以用线性模型进行拟合

只有一个自变量叫一元线性回归，自变量与应变量之间的关系可以用一条直线表示

多个自变量的叫多远线性回归，自变量与应变量之间的关系可以用一个平面或者超平面表示

线性回归的前提条件

A.自变量与应变量之间有线性趋势（皮尔逊相关系数）

B.自变量之间没有关联

对于统计学习来讲机器学习模型就是一个函数表达式，其训练过程就是不断更新这个函数式的参

数，以便这个函数能够多未知数据产生最好的预测结果

线性回归的数学表达式

y=ax+b

y=Wt*X ,常用，其中W,X为列向量,Wt为W转置，

2.最小二乘法：通过最小化残差平方和（数据点与它在回归直线上相应位置的差异称为残差）来找到最佳的函数配比，导数的意义是函数曲线的斜率